chezzzboard
by vishalananth
I’ll also give you the flag if you beat me in chess
nc 2020.redpwnc.tf 31611
Files
Solution
We are given an executable file, on running it we can play chess with ourselves. I tried making some basic moves like e2 To e4 but it was invalid. So, it is time to reverse and see what’s happening. Opening the file with GDB and IDA, we see that it is an enormous chess program with functions to print the board, check the validity of the moves and finally we encouter a function that prints the flag.
Print Board
sub_1B8A -> sub_12B8 -> sub_159A prints chessboard
sub_155B => prints pieces
Check Move Validity
0x5555555555F5 => White move
0x55555555564C => Takes "from" position
rbp + var_74 stores first char of from input - 0x30('0')
rbp + var_70 stores second char of from input - 0x41('A')
first char is subtracted by 8
0x5555555556B7 => Takes "to" position
rbp + var_6C stores first char of to input - 0x30('0')
rbp + var_68 stores second char of to input - 0x41('A')
first char is subtracted from 8
sub_9F4 and a few other functions - checks invalid moves
So we can see that, the proper format for a move is <number><CAPS-Alphabet>
Print Flag
.text:00000000000017DF call sub_2792
.text:00000000000017E4 mov [rbp+var_64], eax
.text:00000000000017E7 lea rax, [rbp+var_40]
.text:00000000000017EB mov rdi, rax
.text:00000000000017EE call __ZNSt7__cxx1112basic_stringIcSt11char_traitsIcESaIcEED1Ev ; std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::~basic_string()
.text:00000000000017F3 cmp [rbp+var_64], 1D3h
.text:00000000000017FA jnz short loc_180F
.text:00000000000017FC lea rdi, command ; "cat flag.txt"
.text:0000000000001803 call _system
We see that, the program calls sub_2792, stores the return value in var_64 and compares it with 1D3h(467). Back tracking the function calls from sub_2792, we realize that every time we give a move a 8*8 loop is run to check each square of the chessboard and apply one of 6 formulas and add that value to temporary variable. Once all 64 iterations are completed the value in the temporary variable is moved to rax and returned. The 6 functions are as follows:
sub_26FC: returns (8-i) + (9+j)
sub_2714: returns multiplication of (8-i)*(9+j)
sub_272C: returns ((8-i)+(9+j))*2
sub_2746: returns remainder of (9+j)/(8-i)
sub_2760: returns (256-(8-i)-(9+j))
sub_27CC: returns (8-i) - (9+j)
where (i,j) is the current square that is being checked.
We find that each piece has its own number assoicated with it which can be found by printing the rax register at this step
.text:00000000000027F3 mov [rbp+var_8], eax
The number for each piece is as follows:
0 - king
1 - queen
2 - bishop
3 - knight
4 - elephant
5 - pawn
6 - empty
We also see that the 6 functions/formulas are chosen based upon what piece is on that particular square we are checking in this iteration. Running and single stepping through the program for a few squares we find the following function associated with each piece.
Rook: (256 - (8-i) - (9+j))
Knight: ((9+j)%(8-i))
Bishop: 2*((8-i)+(9+j))
Queen: (8-i)*(9+j)
King: (8-i) + (9+j)
Pawn: (8-i) - (9+j)
Empty: No function, loop continues to check next square
So we understand that, we have to bring about a specific position on the chessboard in order to make sub_2792, return the value 1D3h, which will then give us the flag.
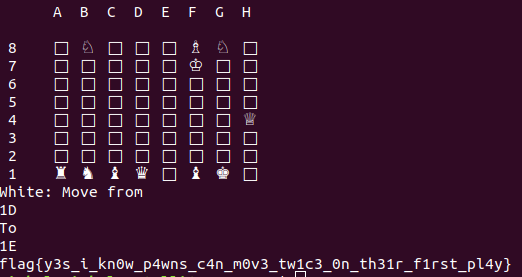
So now we have to find one such position, either using Z3 solver(indicated with 3z’s in chezzz) or manually, that yields 1D3h as the board sum. I did it manually by playing each move, and checking the value of eax register at this step:
.text:00000000000017E4 mov [rbp+var_64], eax
Carefully playing, we can bring the required board sum after a few moves and eventually get the flag. One such position is shown below: